Los números complejos
Diagramas de Argand
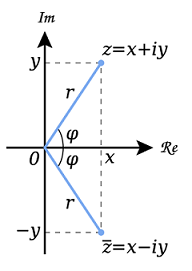
Hay dos representaciones geométricas del número complejo \(z=x+iy\)
- como el punto \(P(x,y)\)
- como el vector \(\overrightarrow{OP}\) del origen a \(P\)
En cada representación, el \(eje-x\) es el eje real y el \(eje-y\) es el eje imaginario. Ambas representaciones son diagramas de Argand de \(x+iy\). En términos de las coordenadas polares de \(x\) y \(y\), se tiene que
y \[z=x+iy=r(\cos \varphi +i \sin \varphi )\]
Definimos el valor absoluto o módulo de un número complejo \(x+iy\) (o su magnitud), como la longitud \(r\) del vector \(\overrightarrow{OP}\), así \[|x+iy|=\sqrt{x^2+y^2} \] Si siempre elegimos las coordenadas polares \(r\) y \( \varphi\) de manera que \(r\) no sea negativo, entonces \[r=|x+iy|\]
El ángulo \( \varphi\) se llama argumento de \(z\) y se escribe como \( \varphi=arg\) \(z\). Por supuesto, cualquier entero múltiplo de \(2 \pi \) pude sumársele a \( \varphi \) para obtener otro ángulo apropiado.
La siguiente ecuación nos da una fórmula muy útil que relaciona un número complejo \(z\), su conjugado \(\overline{z}\) y su módulo \(|z|\) \[z\cdot \overline{z} =|z|^2\]
Producto de números complejos
Si expresamos dos números complejos en términos de sus coordenadas polares, digamos \(z_1=r_1(\cos \varphi_1 +i \sin \varphi_1 )\) y \(z_2=r_2(\cos \varphi_2 +i \sin \varphi_2 )\), entonces el producto de esto dos número complejos se puede expresar como \[z_1z_2=r_1r_2(\cos \varphi_1 +i \sin \varphi_1 )(\cos \varphi_2 +i \sin \varphi_2 )\] Multiplicando término a término, y usando identidades trigonométricas, se llega a que \[z_1z_2=r_1r_2(\cos (\varphi_1+\varphi_2)+i \sin (\varphi_1+\varphi_2))\] que es la expresión de un número complejo con módulo \(r_1r_2 \) y argumento \( \varphi_1+\varphi_2 \)
Potencias de números complejos
El resultado anterior puede extenderse para el producto de \(n\) números complejos. Si los \(n\) números complejos en cuestión son el mismo número, tenemos el número elevado a la \(n\), es decir \(z^n=(r\cos \varphi + i r\sin \varphi)^n\), pero
\[(\cos \varphi + i \sin \varphi)^n=\cos n\varphi + i \sin n\varphi\]
por lo que
\[z^n=r^n(\cos n\varphi + i \sin n\varphi )\]
La segunda igualdad es el enunciado del Teorema de De Moivre.
De lo anterior se deriva que si \(z=r(\cos \varphi + i \sin \varphi) \) es un número complejo distinto de cero, y \(n\) es un entero positivo, entonces hay \(n\) números complejos diferentes entre sí que son raíces \(n-ésimas\) de \(z\). Para ver por qué, tomemos \(w=\rho (\cos \alpha + i \sin \alpha )\), una raíz \(n-ésima\) de \(z\), entonces \(w^n=z\), o \[\rho^n (\cos n\alpha + i \sin n\alpha )=r(\cos \varphi + i \sin \varphi )\] entonces \(\rho=\sqrt[n]{r}\) es la raíz \(n-ésima\) real positiva de \(r\). En cuanto al ángulo, aunque no podemos decir que \(n\alpha\) y \(\varphi\) son iguales, podemos decir que difieren solamente por un entero múltimplo de \(2\pi\). Es decir, \[n\alpha=\varphi+2k\pi\] con \(k=0,\pm 1, \pm2,...\). Entonces\[\alpha=\frac{\varphi}{n}+k\frac{2\pi}{n}\] Por lo que las \(n\) raíces de \(z\) están dadas por \[\sqrt[n]{r(\cos \varphi + i \sin \varphi )}=\sqrt[n]{r}\Bigl(\cos \Bigl(\frac{\varphi}{n}+k\frac{2\pi}{n}\Bigr)+ i \sin \Bigl(\frac{\varphi}{n}+k\frac{2\pi}{n}\Bigr)\Bigr)\]
En la siguiente escena hablaremos acerca de las raíces de un polinomio de grado \(n\).
Créditos
| Diseño del contenido | Elsa Sirenia Vega Camacho |
| Diseño funcional | Elsa Sirenia Vega Camacho |
| Programación | Elsa Sirenia Vega Camacho |
| Asesoría de programación |
Leticia Montserrat Vargas Rocha José Luis Abreu León |
| Diseño gráfico | Ricardo López Gómez |
| Revisión de contenido | Leticia Montserrat Vargas Rocha José Luis Abreu León |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

